Factors Affecting Microbolometer Responsivity

For a more complete discussion of this material, please see:

Jason Lewis, PhD Dissertaion: "Far-Infrared and Sub-Millimeter Microbolometer Detectors," The University of Texas at Austin, 1994.

Abstracted versions of some of our related publications and talks available here on our Web site:



2.2.1 Microbolometer Responsivity

One key figure of merit to consider when designing and optimizing microbolometer performance is responsivity (r), since the signal voltages can be quite low for these devices. A typical bismuth microbolometer has a responsivity of about 20 volts/watt, and noise equivalent power (NEP) on the order of 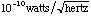. The minimum detectable power will produce a signal in the nano-volt to micro-volt range for measurements taken in the 1-1000 Hz range. Detectors with higher responsivities could ease the amplification requirements in receiver systems by making it easier to detect these small signals. The thrust of the modeling presented here will be toward maximizing the responsivity of antenna-coupled microbolometers.

The signal voltage for a microbolometer can be related to the incident power by using a simple circuit expression for responsivity, given by

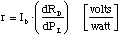(2.14)

where Ib is the dc bias current through the detector, and 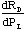is the change in resistance of the detector due power absorption in the load. For conventional bolometers, the load element also acts as the detector. The subscripts allow this expression to also describe composite microbolometer operation, where the load and the detector are separate elements.

According to equation 2.14, the responsivity can be optimized by maximizing the product of Ib and 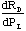. By breaking these terms into physical constants, the role of the material properties becomes much clearer. This relationship with physical properties is dependent on the limiting mechanism of operation. The maximum bias current, for instance, is likely to be limited by one of four things: 1) Thermal Limits of the detector due to I2R (joule) heating, 2) Current density limits in order to avoid electromigration failure in the detector element, or due to the critical superconducting current density in superconducting materials; 3) Bias-induced electric field breakdown across either the detector material or the dielectric between the detector and the load, or 4) Instability of the detector.

2.2.2 Thermally Limited Behavior

A microbolometer will experience heating due to the bias current as well as from incident power. By far, most of the power will come from the bias source across the detector. The maximum allowable temperature rise above ambient ([Delta]Tmax)

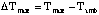(2.15)

due to the maximum allowable dc bias power (Pmax) is

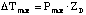(2.16)

where ZD is the thermal impedance of the detector, defined as

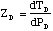(2.17)

Since the power dissipated in the detector is mostly due to joule heating from the bias source, [Delta]Tmax can be represented as

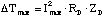(2.18)

The maximum allowable detector bias current (Imax), in terms of the maximum allowed temperature rise, is then

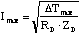(2.19)

The second term in equation 2.14 can be broken down into the following physical constants

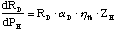(2.20)

where aD is the temperature coefficient of resistivity of the detector material

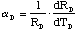(2.21)

[eta]h is defined as the thermal coupling efficiency between the heater and the detector element

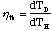(2.22)

and ZL is defined as the thermal impedance of the heater element

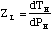(2.23)

For a conventional bolometer, ZL = ZD, and [eta]h = 1.

Substituting equations 2.19 and 2.20 into equation 2.14 reveals a new expression which relates to the physical constants to microbolometer responsivity for the thermally limited case.

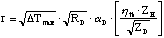(2.24)

The bracketed terms are related, and cannot be varied independently. For convention bolometers, this relation can be reduced to

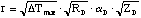(2.25)

The relations in equations 2.24 and 2.25 can be useful in evaluating the potential detector materials and configurations. The square root dependence on [Delta]Tmax shows that the responsivity may be improved by using detector materials that can withstand high temperatures. Materials which are resistant to oxidation and melting would make good candidates. Bismuth, because of its low melting point, is not capable of high temperature operation. [Delta]Tmax could also be increased by lowering the ambient temperature of the system. This is also likely to improve NEP by reducing the thermally-induced component of noise. However, the thermal conductivities of some materials, such as sapphire, increase with decreasing temperature, resulting in lowered thermal impedances. For composite structures, the dielectric layer must also be able to withstand operation at high temperatures. Because [Delta]Tmax has only a square root dependence, however, it is unlikely that this term alone would increase the responsivity by more than a factor of two.

The relations above also indicate that an improvement in responsivity would result from an increase in the thermal impedance of the detectors. It has been shown experimentally that preventing the detector from contacting the substrate by use of air-bridges increases the responsivity of a microbolometer by increasing the thermal impedance of the detector [Neikirk, 1984 #1]. This method was reported to have increased responsivity by a factor of five, and the sensitivity was improved by a factor of four. Choosing detector materials to minimize thermal conductivity would also serve to increase thermal impedances. This criterion would tend to favor semiconductor or oxide materials over metallic detector materials. Choosing a high resistance detector may also be an easy way to increase responsivity. Even though this term has a square root dependence for the thermally limited case, it would be easy to find a detector material with a resistivity of many orders of magnitude higher than bismuth. For conventional microbolometers, the detector resistance is fixed in order to be impedance matched to the antenna. For composite structures, this restriction does not apply. The strong linear dependence of aD on responsivity also makes this a key parameter in detector material choice.


2.2.3 Current Density Limited

Another mechanism which may limit responsivity by limiting the driving current through the detector may be device failure due to electromigration. The current density may also be limited in the case of superconducting microbolometers. In this case, it is assumed that the maximum allowable current is determined by the maximum allowable current density through the detector element, rather than a maximum allowable temperature rise. Although electromigration damage is generally dependent on temperature in most systems, this analysis will assume that the increase in temperature due to the bias current will be small and thus have a negligible effect on the maximum current density.

Equation 2.26 shows an expression for responsivity that is algebraically identical to equation 2.14.

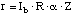(2.26)

The maximum allowable current (Imax) can be related to the maximum current density as

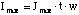(2.27)

where t is the detector thickness, and w is the detector width. The detector resistance can be expressed as

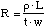(2.28)

where [rho] is the resistivity of the detector material, and L is the physical length of the detector. Substitution of equations 2.27 and 2.28 into 2.26, where Ib = Imax results in the following expression for the dc voltage responsivity.

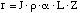(2.29)

For the case of the air-bridge bolometer [Neikirk, 1984 #1], the thermal impedance will be independent of the detector length (see section 2.1.2). For a given detector material, the length of the airbridge will determine the maximum responsivity of the device.

For moderately long substrate supported microbolometers, the thermal impedance is primarily determined by heat flow directly into the substrate. An empirical approximation for this case was presented in section 2.1.3, and is shown in equation 2.11. By using equation 2.11 to approximate Z, the responsivity can be expressed as

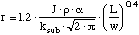(2.30)

This equation will over estimate the responsivity for short detector lengths due to the fringe mechanism of heat loss described in section 2.1.4.

These relations show that for bolometers in which bias current is limited by current density, there is a linear dependence on [rho] as well as a. This criteria would favor bismuth over other metals as a detector material. Materials which are resistant to electromigration would also be favored for this case.

2.2.4 Thermal vs. Current Density

Experiments have shown that typical bismuth microbolometers with the following properties can be operated reliably for long periods of time at 2 milli-amps. The devices become unreliable at around 3 to 5 milli-amps.



length		 4 um
width 2 um
thickness 1500 Å
resistance ~ 100 [Omega]
responsivity ~ 20 volts/watt
a ~ 0.003 K-1

Table 2.4 Operating parameters for a typical bismuth microbolometer

For the dimensions listed in table 2.1, the current density at 0.003 amps would be 106 amps/cm2, which suggests the possibility that failure may be due to electromigration damage.

The temperature rise due to the bias current can be approximated by using

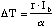(2.31)

This estimates a 20 C temperature rise above ambient (~300 K) when biased at about 0.003 amps. This temperature of ~45 C is much lower that the melting point of bismuth (544 C), which makes it unlikely that failure is due to melting of the bismuth element. Failure due to oxidation is also unlikely if these temperatures are accurate.

Though the observations shown here are not entirely conclusive, they do suggest that electromigration is the most likely mechanism for limiting current in bismuth microbolometers.

2.2.5 Electric Field Breakdown

Composite microbolometers have an extra vulnerability that does not exist with conventional microbolometers, in that voltage differences between the heater and the detector element will result in high electric fields within the dielectric that separates the two elements. The likelihood of accidentally stressing the dielectric may be reduced by grounding one lead of the antenna to one of the detector leads. The dielectric will also experience electric fields due to the detector bias voltage. The electric circuit for electric fields induced by the bias voltage is illustrated in figure 2.9. The highest fields will be at E1, where they will be roughly

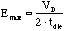(2.32)

where VD is the detector bias voltage, and tdie is the thickness of the dielectric material that separates the heater from the detector.


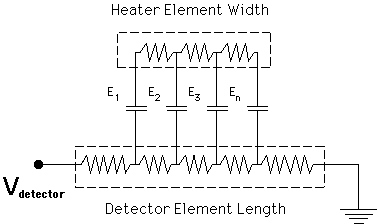
Figure 2.9 Electrical circuit for a composite microbolometer showing the distribution of

electric field within the dielectric.

If electric field-induced breakdown is the limiting factor, then the maximum responsivity can be given as

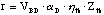(2.33)

where VBD is the breakdown voltage of the device.

This behavior would be more likely for high resistance detectors where high bias voltages (> 10 V) could be used without dissipating much power. For a dielectric thickness of 1000 Å, only 10 volts would be needed to produce an electric field of 106 V/cm, which is about the breakdown field of a good physically-deposited dielectric material. The electric field through the dielectric could be reduced by using a thicker dielectric, but at the expense of lowering the thermal coupling coefficient ([eta]h). Leakage currents through a stressed dielectric may also contribute significantly to signal noise.

2.2.6 Microbolometer Stability

Another issue which affects microbolometer operation and can limit responsivity is stability under constant bias conditions. Using a higher bias across the detector will generally increase responsivity and thus will result in a larger signal. A linear relationship between bias current and responsivity is described in equation 2.14. and implies that it will be linear as long as the other parameters (dR/dT, a, k) remain independent of bias current.

It is important to remember that there are two components of power that are dissipated in the detector. The incident radiation received from the antenna is one component dissipated in the detector, and will be considered an independent variable for this analysis. The other component is power dissipated from the bias current, which will normally be much higher than the incident power. The key point is that incident power (Pincident) can influence the bias power (Pb) by changing the detector resistance. This will result in either positive or negative feedback, depending on whether the device is biased at constant current or constant voltage, and whether the detector has a positive or negative temperature coefficient of resistance.

Table 2.5 shows the conditions which result in positive or negative feedback.



Bias type		 Temp. Coeff. of Resistance Type of Feedback
constant current a > 0 positive
constant current a < 0 negative
constant voltage a > 0 negative
constant voltage a < 0 positive
Table 2.5 Feedback bias relationships

For example, under constant current bias and a positive coefficient of resistance (a > 0), incident power will increase the resistance of the detector. Since the bias current is held constant, this will increase the bias power, thus further increasing the resistance and further increasing the bias power.

Experience has shown that some operating conditions can result in unstable positive feedback where runaway current destroys the device. Instabilities even in large area (100 um x 1000 um) superconducting Bi-Sr-Ca-Cu-O bolometers when operated at high currents have been reported [Lewis, 1989 #5], although these devices were large enough to dissipate a 10 volt bias without destroying themselves. Superconducting devices could be voltage biased in order to avoid positive feedback; however, destructively high currents could occur if the device temperature drifts too close to the superconducting state. In these cases, the maximum bias conditions are lower than what would be predicted when positive feedback effects are ignored. In order to better understand and predict the maximum stable bias, an analysis is given here.

The following definitions will be used for this discussion:

r = small signal responsivity =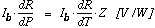

Ib = bias current [I]

Z = Thermal Impedance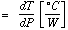

[Delta]Vn = Incremental feedback voltage across detector calculated at nth iteration.

Po = Instantaneous Power at time = 0. (Bias + Incident. Does not include feedback)

[Delta]Pn = Feedback power calculated at nth iteration.

From the above definitions, [Delta]V1, the initial voltage change across the detector due to the bias power and the incident power, can be expressed as:

[Delta]V1 = r . Po (2.34)

The incremental increase in power dissipated in the detector (joule heating) caused by the increased bias voltage can be expressed as:

[Delta]P1 = [Delta]V1 . Ib = r . Po . Ib (2.35)

This increase in power in the detector then causes another incremental increase in detector voltage that can be expressed as:

[Delta]V2 = r . [Delta]P1 = r . Po . [r . Ib] (2.36)

Further iterations of the incremental increases in bias voltage due to feedback can be expressed as:

[Delta]Vn = r . Po . [r . Ib]n-1 (2.37)

The total increase in detector voltage due to feedback can then be expressed as:

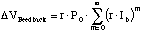(2.38)

By using the following relation:

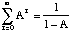for (A < 1) (2.39)

the total feedback voltage can then be expressed as

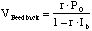(2.40)

From this relation it is apparent that the following must be true for stable operation:

r . Ib < 1 (For stable operation) (2.41)

Another form of this relation looks like:

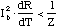
(2.42)

These results suggests that high resistance detectors would be more stable than low resistance detectors. This criterion should be considered when modeling low resistance detectors, such as superconducting microbolometers. However, if high resistance detectors are integrated with a composite microbolometer structure, operation may be limited by electric field breakdown in the dielectric between the heater and the detector.


References

 

1. D. P. Neikirk, W. W. Lam, and D. B. Rutledge, "Far-Infrared Microbolometer Detectors," International Journal of Infrared and Millimeter Waves, 5, 245 - 278 (3 1984).

2. S. M. Wentworth, "Far-Infrared Microbolometer Detectors", Doctoral Dissertation, University of Texas at Austin, 1990

3. V. M. Abrosimov, B. N. Ergorov, and M. A. Krykin, "Size Effect of Kinectic Coefficients in Poly Crystalline Bismuth Films," Sov. Phys. JETP, 37, 113-116 (1 1973).

4. D. P. Neikirk, and D. B. Rutledge, "Air-bridge Microbolometer for Far-infrared Detection," Appl. Phys. Lett., 44, 153-155 (15 January 1984).

5. J. M. Lewis, "Optical Detectors Based on Superconducting Bi-Sr-Ca-Cu-Oxide Thin Films", Undergraduate Thesis, Massachusetts Institute of Technology, 1989